Implicit differentiation made easy
What is implicit differentiation?
Implicit differentiation is a technique used to find the derivative of a dependent variable with respect to an independent variable when the dependent variable is defined implicitly as a function of the independent variable. In other words, it allows you to find the derivative of a function without having to solve for the dependent variable first.
How to use implicit differentiation
To use implicit differentiation, you simply need to follow these steps:
- Differentiate both sides of the equation with respect to the independent variable.
- Solve for the derivative of the dependent variable.
For example, let's say we have the following equation:
``` x^2 + y^2 = 25 ```To find the derivative of y with respect to x, we would first differentiate both sides of the equation with respect to x:
``` 2x + 2y * y' = 0 ```Next, we would solve for y':
``` y' = -x/y ```Benefits of using implicit differentiation
Implicit differentiation has a number of benefits, including:
- It can be used to find the derivative of a function even when the function is not explicitly defined.
- It can be used to find the derivative of a function that is defined implicitly in terms of another function.
- It can be used to find the derivative of a function that is defined implicitly in terms of several variables.
Implicit differentiation calculator
If you're having trouble finding the derivative of a function using implicit differentiation, you can use an implicit differentiation calculator. These calculators can be found online and can be used to find the derivative of any function, regardless of its complexity.
Conclusion
Implicit differentiation is a powerful technique that can be used to find the derivative of a function without having to solve for the dependent variable first. It is a valuable tool for students and mathematicians alike, and can be used to solve a wide variety of problems.
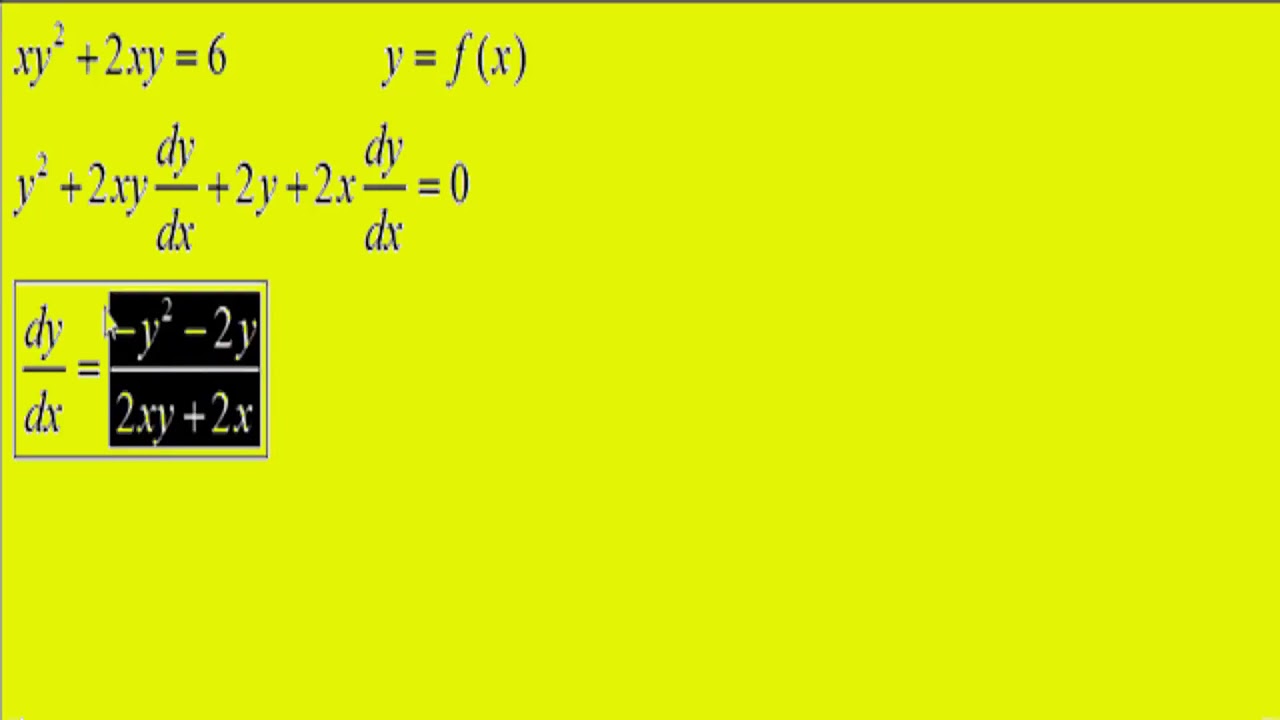

Komentar